Given:
The given quantity of gasoline is Q = 40 gallons.
The big container can hold 5 gallons less than twice the small container.
The objective is to find the number of gallons of each container.
Step-by-step explanation:
Consider the smaller container as S and the larger container as L.
The total quantity of containers can be represented as,

Since the big container can hold 5 gallons less than twice the small container (2S), then the big container L can be represented as,
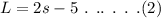
To find S:
Substitute the equation (2) in (1).
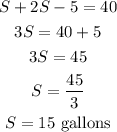
To find L:
Substitute the value of S in equation (1).
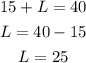
Hence, the small container can hold 15 gallons of gasoline and the large container can hold 25 gallons of gasoline.