Question

8. Nolan wants to save $180 for a new video game system. If he makes $6 a week doing chores, how many weeks will it take him? А 3 weeks B. 30 weeks c. 120 weeks D. 240 weeks

Answer 1

Hello

The cost of the game is $180 and he makes an average of $6 weekly

Let x represent the number of weeks it will take him to save it up

`\begin{gathered} 1\text{ w}eek=6 \\ x=180 \end{gathered}`

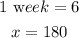
Step 2

Cross multiply both sides and make x the subject of formula

`\begin{gathered} 6* x=1*180 \\ 6x=180 \end{gathered}`

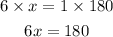
step 3

divide both sides by the coefficient of x

`\begin{gathered} (6x)/(6)=(180)/(6) \\ x=30 \end{gathered}`

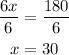
From the calculations above, it will take Nolan 30 weeks to save up for the game. This corresponds to option B