Question

How do i solve y = (x-4)(x+2) by using the method FOIL so i get the standard form

Answer 1

To use the FOIL method, we need to multiply the following terms of each factor:

Firsts: x and x

Outsiders: x and 2

Inner: -4 and x

Lasts: -4 and 2

Multiplying each pair of values and adding the results, we have:

The equation in the standard form is y = x² - 2x - 8, and the coefficients are a = 1, b = -2 and c = -8.

Now, to solve the equation, we need to use the quadratic formula:

`\begin{gathered} x=(-b\pm√(b^2-4ac))/(2a)\\ \\ x=(2\pm√(4+32))/(2)\\ \\ x_1=(2+6)/(2)=(8)/(2)=4\\ \\ x_2=(2-6)/(2)=-(4)/(2)=-2 \end{gathered}`

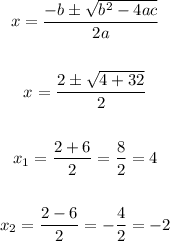
Therefore the solution is x = -2 and x = 4.