Question

Arcs andALGEBRA Find the value of x in each circle.1.384x+10=384x=28QX=74x + 10MР3.А109°A3x + 2B5x7109°

Answer 1

Hello there. To solve this question, we'll have to remember some properties about angles and arcs in a circle.

First case:

So, in the question from the picture, we have the following circle:

We start by making a line pass through A and C.

Notice that the angles in A and C are opposite to the 109º arcs.

This means that:

1. The measures of the angles are equal to 109º/2 = 54.5º

2. Most importantly, the two angles are the same.

With the second information, we know that the triangle ABC is isosceles and the lengths of the sides AB and BC are the same (because they're opposite to angles with the same size)

Thus, we have the following equation:

`\begin{gathered} AB=BC \\ 3x+2=5x-7 \\ 9=2x \\ x=4.5 \end{gathered}`

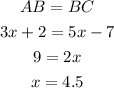
Subtract 3x - 7 on both sides of the equation

Divide both sides by a factor of 2

This is the value of x we've been looking for.