Given:
The equation is given as,

The solutions of the above equation are r and s.
The objective is to find r - s.
Step-by-step explanation:
From the quadratic equation consider a = 2, b = 7 and c = -15.
The solutions r and s can be calculated using quadratic formula as,
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Substitute the value of a, b and c in the above formula.
![\begin{gathered} x=\frac{-7\pm\sqrt[]{7^2-4(2)(-15)}}{2(2)} \\ =\frac{-7\pm\sqrt[]{49+120}}{4} \\ =\frac{-7\pm\sqrt[]{169}}{4} \\ =(-7\pm13)/(4) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9z6fvwe1p93gsi0o50yhrz7k9pmdubstmv.png)
To find r and s:
On further solving the equation,
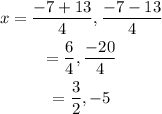
Since, it is given that r > s, the value of r is (3/2) and s is -5.
To find r - s:
Now, the difference can be calcualted as,

Thus, the value of r - s is (13/2).
Hence, option (B) is the correct answer.