Answer:
-√2
Step-by-step explanation:
Given the trigonometric function:
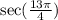
• The function cos is periodical with a period of 2π
,
• The reference angle is an angle less than 2π and that is positive.
We can write this as:
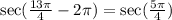
Since the angle π is in the third quadrant, subtract π from it.
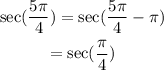
• Secant is the inverse of cosine.
,
• Note that cosine is negative in Quadrant III.
Thus:
![\begin{gathered} \sec \mleft((\pi)/(4)\mright)=(1)/(-\cos \mleft((\pi)/(4)\mright)) \\ =1/-\frac{1}{\sqrt[]{2}} \\ =1*-\sqrt[]{2} \\ =-\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4hqy3tj9tyz498jxfxe9i0vgebbh7zaygn.png)
Therefore:
![\sec ((13\pi)/(4))=-\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/j7xrcv6luskd09gxqafsyfck4lbp15layn.png)