From the question
Perimeter of rectangular perian rug = 30ft
Area of rectangular persian rug = 54 ft square
We are to find length and width of the persian rug
let, length of pertianrug = l
width of persian rug = w
Recall perimeter P of a rectangle is given as

Since perimeter = 30ft then
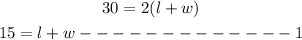
Also, recall area A of a rectangle is given as
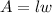
But area = 54ft square then
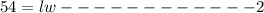
Making l the subject in equation 2 we have

Substitite for l into equation 1, we have
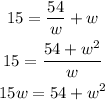
This then gives
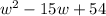
By solving the quadraric equation we get
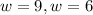
Net we are to solve for l
From equation 3
When w = 9
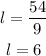
when w = 6
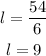
This implies that
l=6 when w = 9
l = 9 when w = 6
Finally
The length(longer side of the triangle is 9ft while