SOLUTION:
Step 1:
In this question, we are given the following:
Barbara has a bunny that weighs 2 pounds and gains 3 pounds
per year which means:
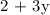
Her cat weighs 6 pounds and gains 1 pound per year which means:
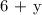
When will the bunny and the cat weigh the same amount means:

collecting like terms, we have that:

CONCLUSION:
The bunny and the cat will weigh the same amount in 2 years' time.