The given polynomial is
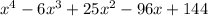
Using Desmos online graphing calculator, the graph of the function is shown below
From the graph, a zero of the polynomial occurs at the point (3,0)
Hence x = 3 is a zero of the polynomial
Hence x = 3
This implies that x - 3 is a factor of the polynomial
Using synthetic division to verify the zeros
Perform the division
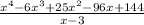
The division is shown below
Since the remainder of the polynomial is 0, hence 3 is a zero of the polynomial
Factoring the polynomial gives
Since x - 3 is a factor then
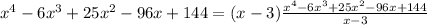
From the synthetic division
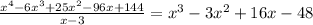
It follows
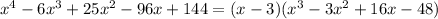
Factoring

gives
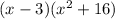
It follows
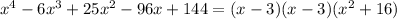
Hence the imaginary zeros occur at
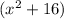
Equate to zero and solve
![\begin{gathered} x^2+16=0 \\ \Rightarrow x^2=-16 \\ \Rightarrow x=\pm\sqrt[]{-16}_{} \\ x=\pm4i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4jrgp856e2js1qffprhgua8vpnh4rtu2e6.png)
Therefore, the imaginary zeros are 4i and -4i