Question

The Lake of Distress is contaminated with flesh-eating bacteria!! The lake started withonly 4 square feet infected, but as time has gone on, the bacteria are growing by a factorof 3 every hour. The relationship between the bacteria and time is...Linear0 Exponential

Answer 1

Data

t = time

N = sqare of feet infected

t=0 N=4

t=1 N= 3(4) =12

If every hour the sqare infected grow 3 times the previus hour it means that if we calculate the data for some hours it will be like this:

`t_0=0;N_0=4`
`t_1=1;N_1=\text{ (3)4=12}`
`t_2=2;N_2=(3)12=36`
`t_3=0;N_3=3(36)=108`

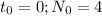
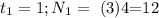
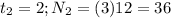
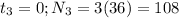
You can notice that the form growth occurs is:

`N_n=3(N_(n-1))`

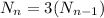
where:

N is the sqare of feet infected

n is the numbner of the data related with the hours

Nn-1 is the square of feet infected is the las hour

If we put this in a graph it will be:

Seeing the graphic we can conclude that it is an exponential growing