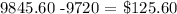Question

Logan and Rita each open a savingsaccount with a deposit of $8,100. Logan'saccount pays 5% simple interest annually.Rita's account pays 5% interestcompounded annually. If Logan and Ritamake no deposits or withdrawals over thenext 4 years, what will be the difference intheir account balances?$125.60$104.05$113.22$134.89

Answer 1

`\text{ \$125.60}`

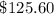
Step-by-step explanation:

Here, we want to get the difference in the account balance of two people. One who deposits with a simple interest return and another with a compound interest return

For Logan:

`\begin{gathered} Amount\text{ = Interest\lparen I\rparen + Principal\lparen P\rparen} \\ I\text{ = }(PRT)/(100) \\ \\ A\text{ = }(PRT)/(100)\text{ + P} \\ \\ A\text{ = P\lparen}(RT)/(100)+\text{ 1\rparen} \end{gathered}`

Where P is the amount deposited which is $8,100

R is the rate which is 5%

T is the time which is 4 years

Substituting the values:

`\begin{gathered} A\text{ = 8100\lparen}(5*4)/(100)\text{ + 1\rparen} \\ \\ A\text{ = 8100\lparen0.2+1\rparen} \\ A\text{ = 8100\lparen1.2\rparen} \\ A\text{ = \$9,720} \end{gathered}`

For Rita:

Here, we want to get the amount for a compounding deposit type

`A\text{ = P\lparen1 + }(r)/(n))\placeholder{⬚}^(nt)`

where P is the principal which is $8,100

r is the rate which is 5% = 5/100 = 0.05

n is the number of times interest is compounded yearly which is 1 (since it is annual)

t is the number of years which is 4

Substituting the values, we have it that:

`\begin{gathered} A\text{ = 8100\lparen1 + }(0.05)/(1))\placeholder{⬚}^(4*1) \\ A\text{ = 8100\lparen1.05\rparen}^4\text{ = \$9,845.60} \\ \end{gathered}`

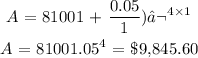
Finally, we proceed to get the difference

Mathematically, we have that as:

`9845.60\text{ -9720 = \$125.60}`