We have the following:
The line passes through the coordinates (7, 0):
The line is parallel to the equation:
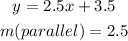
We will find the equation of the line as shown below:
I. Find the slope of the line, we have:
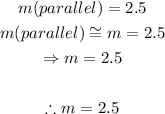
II. We will use the point-slope equation to obtain the equation of the line as shown below:
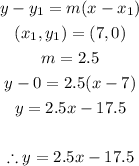
T