To answer this question, we need to have into account the formula for the volume of a cylinder. This formula is given by:

1. We have that pi is approximately equal to 3.1415926535...
2. The radius is half of the diameter. In this case, the diameter is 6 feet. Therefore, the radius is 3 feet.
3. The height of the storage tank (cylinder) is h = 10 feet.
Hence, we can plug all of these values into the formula, and we can get the value for the total volume of this cylinder:
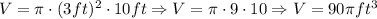
Now, since the tank is half-filled with oil, we have that the oil, in cubic feet, in the cylindrical tank is half of the value of the previous value, that is:
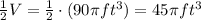
Hence, the current volume of oil in the cylindrical tank is:

(Option C).