Given the mass of a radioactive substance after time t days is given by
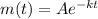
The initial mass of the substance is 120 milligrams, which means m(0)=120. So,
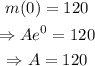
The mass of the substance is 90 milligrams after 10 days, which means m(10)=90. So,
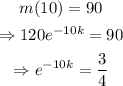
Now, take natural logarithm on both the side and use the property
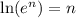
So, the above equation will become
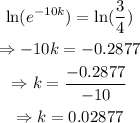
Therefore, the relation between the mass of the substance at time t days is given by t
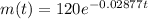
The mass of the substance after 16 days will be
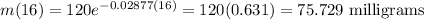
The day during which the mass of the substance reaches 50 milligrams can be obtained as follows:
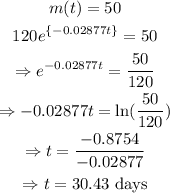
The graph that shows the relationship between m and t is given below: