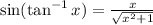Given:
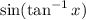
To write:
The trigonometric function in terms of x.
Step-by-step explanation:
Let us take,
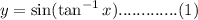
Let us assume that,
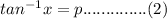
So, the function becomes

From the equation (2),
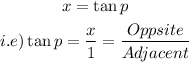
Using Pythagoras theorem,
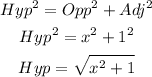
So, equation 3 becomes,
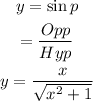
Therefore, the composed trigonometric function in terms of x is,
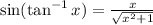
Final answer:
The composed trigonometric function in terms of x is,