Question

Find a fifth-degree polynomial with integer coefficients that has zeros -5i and 2, with 2 a zero of multiplicity 3. Do not foil out! Leave in factored form.

Answer 1

(x+25)(x-2)^3

Explanation:

A multiplicity of a root means how many times it appears in the polynomial equation.

For example, if we have a polynomial equation (x - a)^n = 0, n is the multiplicity of the root a because it gives us this root n times.

Hence, because we are told that the root x =2 is of multiplicity 3, then we know that the following term must appear in the polynomial equation

`(x-2)^3`

Furthermore, we are also told that the polynomial equation has the root -5i, this implies that the following term must also appear in the equation

`(x^2+25)`

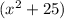
because when we equate it to 0, the above will give

`x^2+25=0`

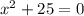
the roots come out to be

`x=\pm5i`

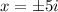
Hence, the fifth-degree polynomial equation looks like

`(x^2+25)(x-2)^3=0`

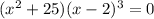
which is our answer!