Given:
Perimeter of rectangle = 220 inches
Ratio of length to width = 7:3
Use the perimeter of a rectangle formula:
P = 2(L + W)
220 = 2(L + W)
Divide both sides by 2:

Take the ratio:
7W : 3L
7W = 3L
Divide both sides by 3:
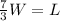
Substitute 7/3 W for L in (110 -W = L)
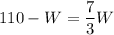
Multiply through by 3:
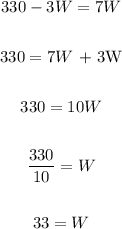
To find L, we have:
110 - W = L
110 - 33 = L
77 = L
To find the Area, use the formula:
Area = Length x Width
Area = 77 x 33 = 2541 square inches
ANSWER:
2541 square inches