![\begin{gathered} 1)5\pm\sqrt[]{13} \\ 2)D \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qbtkis2xbh661swze3wix40uy84i5ka3fw.png)
1) We can rewrite that equation to solve it in a clear way:
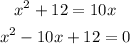
This way we can clearly see the coefficients. Let's solve that quadratic:
![\begin{gathered} x=\frac{-b\pm\sqrt[]{\Delta}}{2a}=\frac{10\pm\sqrt[]{100-48}}{2}= \\ x_1=5+\sqrt[]{13} \\ x_2=5-\sqrt[]{13} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7lke4wve4jdegmpi2mrwowrqika4ph2mae.png)
2) To find out the number of solutions for this equation, let's calculate the
value of the discriminant:
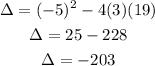
Whenever we have a negative value for the discriminant then we have Complex roots
3) Hence, the answer is:
![1)5\pm\sqrt[]{13}](https://img.qammunity.org/2023/formulas/mathematics/college/wceinseas8kkzdmf6t4wtxq2a7cp7b8brg.png)
2) 2 Complex (Nonreal) Roots