Question

A book store is charging $3 for paperback books and $9 for hardback booksDionte creates two patterns to compare the costs. He writes ordered pairs in the form (paperback cost, hardback cost) for corresponding numbers of books. Which orderedpairs could be on Dionte's list?Choose all that are correct.(627)(12, 36)(15,45)(18,54)(24,81)

Answer 1

If Dionte creates a list, it will be (3*n, 9*n) where "n" is the number of books, then, we have the pattern:

`(3n,9n)\quad n\in\mathbb{N}`

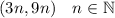
But how do discover which one should be on the list? See that the first coordinate is divisible by 3, if we divided it by 3 we have just "n", if we do divide the second coordinate by 9 we have just "n" as well. Then we have to divide by three the first coordinate and by 9 the second one, after that they must be the same! if they are the same it's correct.

a)

`(6,27)_{}`

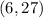
Let's do our logic, divide by 3 and the other by 9

`((6)/(3),(27)/(9))=(2,3)`

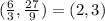
As we can see it's different, so it couldn't be on Dionte's list.

b)

Doing the same thing

`((12)/(3),(36)/(9))=(4,4)`

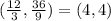
The result is (4,4), two equal numbers, then it could be on Dionte's list.

c)

`((15)/(3),(45)/(9))=(5,5)`

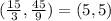
The result is (5,5), two equal numbers, then it could be on Dionte's list.

d)

`((18)/(3),(54)/(9))=(6,6)`

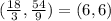
The result is (6,6), two equal numbers, then it could be on Dionte's list.

e)

`((24)/(3),(81)/(9))=(8,9)`

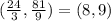
Here we have a different result again, then it couldn't be on Dionte's list.