The sets in the alternatives are contained into each other.
The Real Numbers contains all the other sets. This means that if it is in one of the other sets, it is also in the Real Numbers.
The Real numbers have the Irrational Numbers and, separately, the Rational Numbers.
The Rational Numbers is the set that contains all numbers that can be written as:

Suche that p is an integer and q is an integer different than 0.
In this case, the number
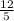
Is written in this form, because 12 and 5 are integers and 5 is not equal to 0.
This means that 12/5 is a Rational Number.
The Integer Numbers are numbers that are whole and can be negative. However, we can't write 12/5 as a whole number, because it is decimal.
The Whole Numbers are contained in the Integer Numbers, so 12/5 is in neither of them.
Also, every Rational Number is not an Irretional Number, so since 12/5 is a Rational Number, it doesn't belong to the Irrational Numbers.
So, in the end, we have the answer:
12/5 belongs to the Rational Numbers and, thus, to the Real Numbers. It doesn't belong to any other in the list.