We have to calculate the midpoint for each segment.
To do that we have to calculate the average for the coordinates of each point.
1) For AB, we have A = (-5,8) and B = (-5,6).
We can then calculate the midpoint coordinates as:
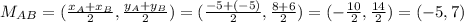
2) For BC we have B = (-5,6) and C = (-2,6).
The midpoint will be:
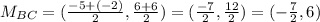
3) For CD we have C = (-2,6) and D = (2,3).
The midpoint will be:
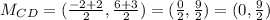
4) For DE we have D = (2,3) and E = (2,-1).
The midpoint will be:
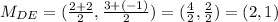
5) For EF we have E = (2,-1) and F = (6,0).
The midpoint will be:
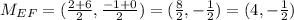
Answer:
AB = (-5,7)
BC = (-7/2,6)
CD = (0,9/2)
DE = (2,1)
EF = (4,-1/2)