Question

A company has 9 male and seven female employees and needs to nominate two men and two women for the company bowling team how many different teams can be formed?

Answer 1

Step-by-step explanation

The number of different teams that can be formed is given by the product of two numbers:

1. The number of different ways that 2 male employees can be selected.

2. The number of different ways that 2 female employees can be selected.

The first number is given by all the possible ways to select 2 males out of 9 without caring about the order. This last part basically means that even though there are two ways to select two particular males (let's name them A and B), which are AB and BA, they count as a single way. This implies that what we are looking for is the total number of combinations. In general, the total number of combinations when selecting k items from a total of n is given by:

`_nC_k=(n!)/((n-k)!k!)`

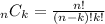
Then the number of different ways that 2 male employees can be selected is given by:

`_9C_2=(9!)/((9-2)!2!)=(9!)/(7!2!)=36`

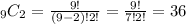
For the number of different ways that 2 female employees can be selected we can do the same. The only difference is that here we have a total of 7 people to select from:

`_7C_2=(7!)/((7-2!)2!)=(7!)/(5!2!)=21`

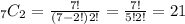
Then the number of different teams that can be formed is given by the product of the two numbers that we found:

`N=36\cdot21=756`Answer

Then the answer is 756.