Question

What is the measure of angle QRS in this figure?A:78B:120C:132D:175

Answer 1

Step 1:

Concept: Use the two theorems below to find the measure of angle QRS

1. The sum of angles in a triangle is 180 degrees

2. The sum of angles on a straight line is 180 degrees.

Step 2:

Angle QRP is on a straight line with angle QRS = 20x + 12

`\begin{gathered} m\text{QRP + mQRS = 180} \\ m\text{QRP + 20x + 12 = 180} \\ m\text{QRP = 180-12-20x} \\ m\text{QRP = 168 - 20x} \end{gathered}`

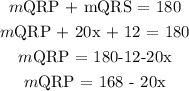
Step 3:

Sum of angles in a triangle = 180

`\begin{gathered} 9x\text{ + 13x + 168 - 20x = 180} \\ \text{Collect similar terms} \\ 9x\text{ + 13x - 20x = 180 - 168} \\ 2x\text{ = 12} \\ \text{x = }(12)/(2) \\ \text{x = 6} \end{gathered}`

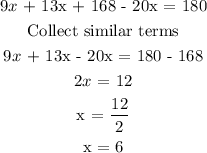
Final answer

m

= 20(6) + 12

= 120 + 12

= 132 Option C