Question

I need help with this question, please. This is non graded.

Answer 1

The rule of the volume of the rectangular prism is

`V=L* W* H`

L is the length

W is the width

H is the height

From the attached picture we can see

L = (2x - 3)

W = (x + 1)

H = (3x + 4)

We will substitute them in the rule above

`V=(2x-3)(x+1)(3x+4)`

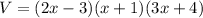
We will multiply the first 2 brackets, then multiply the answer by the 3rd bracket

`\begin{gathered} (2x-3)(x+1)=(2x)(x)+(2x)(1)+(-3)(x)+(-3)(1) \\ (2x-3)(x+1)=2x^2+2x-3x-3 \\ (2x-3)(x+1)=2x^2-x-3 \end{gathered}`

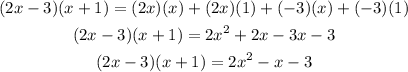
Multiply this answer by the 3rd bracket

`\begin{gathered} (2x^2-x-3)(3x+4)= \\ \left(2x^2\right)\left(3x\right)+\left(2x^2\right)\left(4\right)+\left(-x\right)(3x)+(-x)(4)+(-3)(3x)+(-3)(4)= \\ 6x^3+8x^2-3x^2-4x-9x-12= \\ 6x^3+5x^2-13x-12 \end{gathered}`

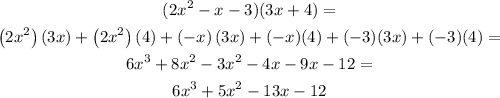
Then the volume of the prism is

`V=6x^3+5x^2-13x-12`

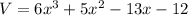
The answer is the 2nd choice