Given the Quadratic Equation:
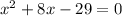
You can identify that it has this form:
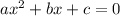
The Quadratic Formula is:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
In this case:
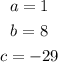
Then, you can substitute values into the Quadratic Formula and simplify:
![\begin{gathered} x=\frac{-(8)\pm\sqrt[]{(8)^2-(4)(1)(-29)}}{2\cdot1} \\ \\ x=\frac{-8\pm\sqrt[]{180}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4kd9b8jne6l8dtrm8kj5a7u7ilxiayuzzc.png)
Notice that the symbol ± indicates that you actually have these two equations:
![\begin{gathered} x_1=\frac{-8+\sqrt[]{180}}{2} \\ \\ \\ x_2=\frac{-8-\sqrt[]{180}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/f3zuakxamb9hniegf9rodv957ldtf8apc8.png)
Therefore, evaluating, you get:
![\begin{gathered} x_1=-4+3\sqrt[]{5} \\ \\ x_2=-4-3\sqrt[]{5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mtk9q3px492pay1e0otslyisvnkdpnm4yl.png)
Hence, the answer is:
![\begin{gathered} x_1=-4+3\sqrt[]{5} \\ \\ x_2=-4-3\sqrt[]{5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/mtk9q3px492pay1e0otslyisvnkdpnm4yl.png)