Question

Question is in picture. The percentage of Job is 18%,

Answer 1

Given the bar graph that shows the percentage of adults that use the internet for specific tasks, you can identify that these are:

`E-mail=34\text{\%}`
`Information\text{ }Searches=29\text{\%}`
`News=25\text{\%}`
`Job=18\text{\%}`
`School=13\text{\%}`

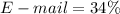
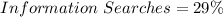
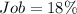
By definition, the Roster Method is used to list the elements of a set in a row inside curly brackets.

In this case, you know that "x" is a task in which usage lies between 15% and 33%. Therefore, you have to list all the tasks whose percentages are between 15% and 33%:

`\lbrace Information\text{ }Searches,News,Jobs\rbrace`

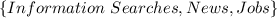
Hence, the answer is: First option.