Question

A projectile is launched upward. The function f(x)=-16x2 + 64x describe the position of the projectiles height, in feet, x seconds after it is launched.

Answer 1

Given:

`f(x)=-16x^2+64x`

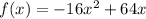
Differentiate with respect to x, we get

`f^(\prime)(x)=-16*2x+64(1)`

`f^(\prime)(x)=-32x+64`
`\text{Set f'(x)=0 to find the maxi}mum\text{ value of x}`

`0=-32x+64`

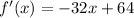
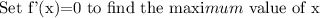
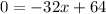
Adding 32x to both sides of the equation, we get

`0+32x=-32x+64+32x`

`32x=64`

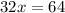
Dividing both sides by 32, we get

`(32x)/(32)=(64)/(32)`
`x=2`

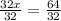
We get the maximum value of x is 2.

Substitute x=2 in the given function to find the maximum height of the projectiles.

`f(2)=-16(2)^2+64*2`

`f(2)=64`

Hence the maximum height of the projectiles is 64 feet.

Substitute f(x) =0 in the given function to find the number of seconds the rocket takes to hit the ground.

`0=-16x^2+64x`

`0=-16x(x-4)`

`x=0\text{ or (x-4)=0}`
`\text{Consider x-4=0.}`
`x=4\text{ }`

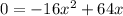
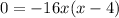
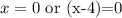
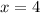
After 4.0 seconds, the rocket hit the ground.