Question

Use the concept of the definite integral to find the total area between the graph off(x) and thex-axis, by taking the limit of the associated right Riemann sum. Write the exact answer. Do not round. (Hint: Extra care isneeded on those intervals wheref(x) < 0. Remember that the definite integral represents a signed area.)f(x) = 3x + 3 on [0, 2]

Answer 1

15 square unit.

Step-by-step explanation

Step 1:

Recall that the right endpoint Riemann sum for

`\begin{gathered} ^{}\int ^b_af(x)dx\text{ is given by } \\ (b-a)/(n)\sum ^n_(k\mathop=1)f(a+(b-a)/(n)k) \end{gathered}`

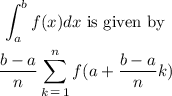
Step 2:

Note, if f(x) is continuous, then:

`\lim _(n\to\infty)(b-a)/(n)\sum ^n_{k\mathop{=}1}f(a+(b-a)/(n)k)\text{ = }^{}\int ^b_af(x)dx\text{ }`

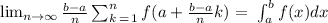
Step 3:

Now, applying the limit of the Reimann sums to evaluate the integral:

`^{}\int ^2_0(3x+3)dx\text{ }`

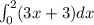
Please, carefully check my working:

Hence, using the concept of the definite integral, the total area between the graph of f(x) and the x-axis by taking the limit of the associated right Riemann sum is 15 square unit.