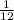Given:
There are four cards numbered
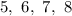
Required:
We have to find the probability of picking an 8 and then picking a 5.
Step-by-step explanation:
The possibility of picking an 8 in the first time is 1 out of the four cards.
Therefore the probability of picking an 8 first is
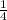
Now since you did not put the card back so there are three cards now.
So the possibility of picking a 5 in the second time out of the three cards is 1.
Therefore the probability of picking a 5 in the second time is

Now we multiply both the probabilities to find the required answer.
Hence the probability of picking an 8 and then a 5 is
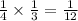
Final answer:
Hence the final answer is