To find the area of the shaded region, we have to subtract the area of the parallelogram and the area of the rectangle. Let's find the area of each figure.
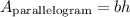
The base of the parallelogram is 4m and the height is 6m.
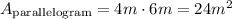
Now let's find the area of the rectangle.
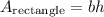
The base of the rectangle is 3m and the height is 2m.
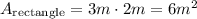
Once we have the area of each figure, let's subtract.
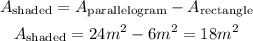
Therefore, the area of the shaded region is 18 m^2.