The given function is

First, we have to find the vertex. So, let's solve the product.
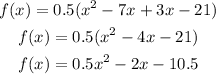
Where a = 0.5 and b = -2. Let's find the horizontal coordinate of the vertex
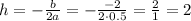
Then, we find the vertical coordinate of the vertex
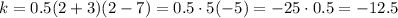
The important thing about the vertex is that the coordinate k tells us the maximum or minimum. In this case, the function has a minimum at -12.5 because that's the lowest point reached by the function. The image below shows the graph