Remember that
the difference quotient is equal to
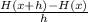
we have
H(x)=(1/3)x^2-2
so
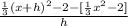
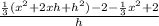
Simplify
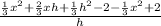
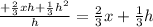
For h=0.1
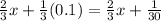
For h=0.01
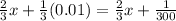
For h=0.001

Find out the slope at the point (6,10)
For x=6
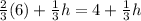
For h=0.1
slope is
4+1/30=4+0.033333=4.033333
For h=0.01
4+1/300=4+0.003333=4.003333
For h=0.001
4+1/3,000=4+0.000333=4.000333
the slope is 4 at point (6,10)