Question

Can someone help me out please please

Answer 1

To answer this question we will use the following property of logarithms:

`\ln a^b=b\ln a.`

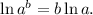
Dividing the given equation by 4 we get:

`(4*8^x)/(4)=(11.48)/(4).`

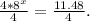
Simplifying the above result we get:

`8^x=2.87.`

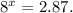
Applying the natural logarithm we get:

`\ln8^x=\ln2.87.`

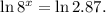
Applying the property of logarithms we get:

`x\ln8=\ln2.87.`

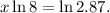
Therefore:

`x=(\ln2.87)/(\ln8)\approx0.51.`

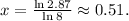
Answer: Option D.