Question

Given points A (3, -6, 2), B (6, -7, -1) and C (0, -1, 5)(a) Find the component form of the vectors u (from A to B) and v (from A to C)(b) The angle between vectors u and v.Show all your work.

Answer 1

Given:

A: (3, -6, 2)

B: (6, -7, -1)

C: (0, -1, 5)

Find:

a. component form of the vectors u (from A to B) and v (from A to C)

b. The angle between vectors u and v.

Solution:

a. In order to get the component of the vector u (from A to B), we simply have to subtract each corresponding component of A from B. Thus, we have:

`(6-3,-7--6,-1-2)`
`VectorU=(3,-1,-3)`

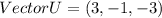
For Vector V which is from A to C, we simply have to subtract each corresponding component of A from C.

`(0-3,-1--6,5-2)`
`VectorV=(-3,5,3)`

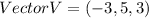
The component form of Vector U is (3, -1, -3) while Vector V is (-3, 5, 3).

b. To determine the angle between them, here are the steps:

Calculate the dot product of Vector U and V by getting the sum of the product of each corresponding component of U and V.

`(3*-3)+(-1*5)+(-3*3)`
`-9+(-5)+(-9)\Rightarrow-23`

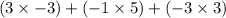
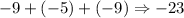
The dot product is -23.

Next, calculate the magnitude of each vector.

To get the magnitude of a vector, square each component of the vector and add them. After that, get the square root of the sum.

`|u|=√(x^2+y^2+z^2)\Rightarrow|u|=√(3^2+(-1)^2+(-3)^2)`
`|u|=√(9+1+9)\Rightarrow|u|=√(19)`

The magnitude of vector u is √19.

`|v|=√((-3)^2+5^2+3^2)\Rightarrow|v|=√(9+25+9)\Rightarrow|v|=√(43)`

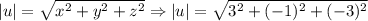
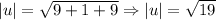
The magnitude of vector v is √43.

Multiply the magnitude of vectors u and v.

`√(19)*√(43)=√(817)`

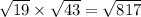
Divide the dot product by the product of the two magnitudes.

`-23/√(817)=-0.8046681428`

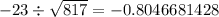
Then, multiply the inverse of cosine by the result above.

`\begin{gathered} \theta=cos^(-1)(-0.8046681428) \\ \end{gathered}`
`\theta=143.578\approx143.58\degree`

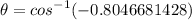
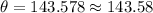
The angle between Vector U and V is approximately 143.58°.