We have to find the x-intercept and y-intercept in each equation.
The x-intercept is the value of x where the function intersects the x-axis. It corresponds to the value y=0, as that is the value of y where the x-axis is located.
The y-intercept is like the x-intercept but for the y-axis and corresponds to a value x=0.
We can see an example in a graph before solving each point:
51) We can use the fact that for the x-intercept the value of y is 0. If we replace this in the equation, we can clear the value of x that correspond to the x-intercept:
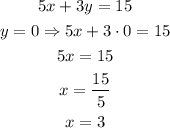
The same can be don for the y-intercept, where x=0:
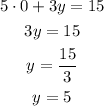
Then, the x-intercept is located at (3, 0) and the y-intercept is located at (0, 5).
54) We apply the same procedure as 51):
X-intercept (y=0)
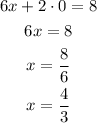
Y-intercept (x=0)
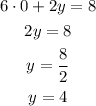
Then, the x-intercept is at (4/3, 0) and the y-intercept is at (0, 4).
56)
X-intercept (y=0)
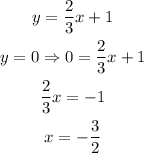
Y-intercept (x=0)
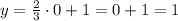
The x-intercept is at (-3/2, 0) and the y-intercept is at (0, 1).
Answer:
51) x-intercept at (3, 0) and y-intercept at (0, 5)
54) x-intercept at (4/3, 0) and y-intercept at (0, 4)
56) x-intercept at (-3/2, 0) and y-intercept at (0, 1)