Question

Find the slop of the line passes thought point (9-8) and (2-1)

Answer 1

The points we have are:

(9,-8) and (2,-1)

And we need to find the slope between the two points.

Step 1. Label the coordinates as follows:

`\begin{gathered} x_1=9 \\ y_1=-8 \\ x_2=2 \\ y_2=-1 \end{gathered}`

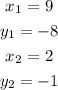
Step 2. Use the slope formula:

`m=(y_2-y_1)/(x_2-x_1)`

Where m is the slope.

Step 3. Substitute the values of x1, y1, x2, and y2:

`m=(-1-(-8))/(2-9)`

Step 4. Solve the operations to find the slope.

First, we simplify the numerator as follows:

`m=(-1+8)/(2-9)`

Because -(-8) is equal to +8.

Next, We make the addition on the numerator and the subtraction on the denominator of the expresion:

`m=(+7)/(-7)`

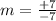
Finally, we make the division +7 by -7 which results in -1:

`m=-1`

The slope between the points is 1.

Answer: 1