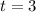Given:
The height of the rocket after t second taking off is given by the formula,
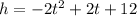
Required:
We need to find the time when the rocket hit the ground.
Step-by-step explanation:
We know that the greatest height is zero when the rocket hit the ground.
Substitute h =0 in the given equation to find the time when the rocket hit the ground.
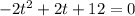
Divide both sides of the equation by (-2).
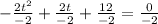
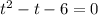

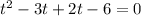
Taking out the common term.
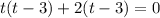
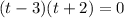
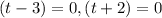
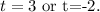
The time should not be of negative value.