Question

A cash register contains only five dollar and ten dollar bills. It contains twice as many five's as ten'sand the total amount of money in the cash register is 720 dollars. How many ten's are in the cashregister?

Answer 1

Step-by-step explanation

Step 1

Set the equations:

let x represents the number of five dollars bills

let y represents the number of ten dollars bill

so

a)It contains twice as many five's as ten's,so

`x=2y\Rightarrow equation(1)`

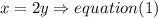
b)and the total amount of money in the cash register is 720 dollars,so

`5x+10y=720\Rightarrow equation(2)`

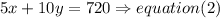
Step 2

solve the equations:

`\begin{gathered} x=2y\Rightarrow equation(1) \\ 5x+10y=720\Rightarrow equation(2) \end{gathered}`

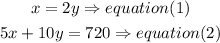
a)replace the y value from eq(1) into equation(2)

hence

`\begin{gathered} 5x+10y=720\Rightarrow equation(2) \\ 5(2y)+10y=720 \\ 20y=720 \\ divide\text{ both sides by 20} \\ (20y)/(20)=(720)/(20) \\ y=36 \end{gathered}`

b) replace the y value into equation(1) to obtain x

`\begin{gathered} x=2y \\ x=2(36) \\ x=72 \end{gathered}`

therefore,

the number of five dollars bill is : 72

the number of ten dollars bill is : 36

I hope this helps you