Question

Find the slope of a line that is a) parallel and b) perpendicular to the given line.3x + 2y = -3

Answer 1

(a)

The given equation of a line is,

`3x+2y=-3\text{ ---(1)}`

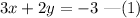
The general equation of a straight line is given by,

`y=mx+c\text{ }---(2)`

Here, m is the slope of the line and c is the y intercept.

Rewrite equation (1) into the form of equation (2).

`\begin{gathered} 2y=-3x-3 \\ y=(-3)/(2)x-(3)/(2)\text{ ---(3)} \end{gathered}`

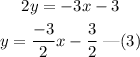
Comparing equations (1) and (3), we get the slope of the line m=-3/2.

Two parallel lines has the same slope. So, the slope of a line parallel to the line 3x+2y=-3 with slope m=-3/2 is -3/2.

(b)

The slope of a line perpendicular to the line with slope m=-3/2 is,

`M=(-1)/(m)=(-1)/(-(3)/(2))=(2)/(3)`

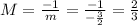
Therefore, the slope of a line perpendicular to 3x+2y=-3 with slope m=-3/2 is 2/3.