Question

Form a polynomial whose zeros and degree are given. Use a leading coefficient of 1. Zeros: -1, 1, - 5; degree 3Af(x) = x3 + 5x2 - x - 5Bf(x) = x3 + 5x2 + x + 5Cf(x) = x3 - 5x2 + x - 5Df(x) = x3 - 5x2 - x + 5

Answer 1

By definition:

- The zeros of a function are also called roots and x-intercepts.

- The highest exponent of the variable of the function indicates the degree of the function.

In this case, knowing that the zeros of the function are:

`\begin{gathered} x=-1 \\ x=1 \\ x=-5 \end{gathered}`

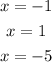
You can write it in the following factored form:

`f(x)=(x+1)(x-1)(x+5)`

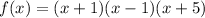
Simplifying it, you get:

`\begin{gathered} f(x)=(x+1)(x-1)(x+5) \\ f(x)=(x^2-1)(x+5) \\ f(x)=(x^2)(x)+(x^2)(5)-(1)(x)-(1)(5) \\ f(x)=x^3+5x^2-x-5 \end{gathered}`

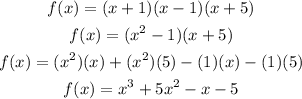
Hence, the answer is: Option A.