Question

2x+3y + 2z=14-3x+2y+z=274x + 5y – 4z = 28

Answer 1

x=-4, y=8 and z=-1.

Step-by-step explanation:

Given the system of equations:

`\begin{gathered} 2x+3y+2z=14 \\ -3x+2y+z=27 \\ 4x+5y-4z=28 \end{gathered}`

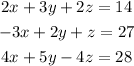
Step 1: Make z the subject in the second equation.

`\begin{gathered} -3x+2y+z=27 \\ z=27+3x-2y \end{gathered}`

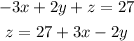
Step 2: Substitute z into the first and third equations.

First equation

`\begin{gathered} 2x+3y+2z=14 \\ 2x+3y+2(27+3x-2y)=14 \\ 2x+3y+54+6x-4y=14 \\ 2x+6x+3y-4y=14-54 \\ 8x-y=-40 \\ \implies y=8x+40 \end{gathered}`

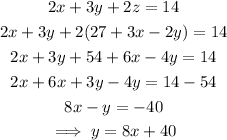
Third equation

`\begin{gathered} 4x+5y-4z=28 \\ 4x+5y-4(27+3x-2y)=28 \\ 4x+5y-108-12x+8y=28 \\ 4x-12x+5y+8y=28+108 \\ -8x+13y=136 \end{gathered}`

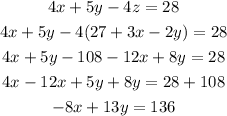
Step 4: Substitute y=8x+40 (first equation) into -8x+13y=136 (third equation).

`\begin{gathered} -8x+13y=136 \\ -8x+13(8x+40)=136 \\ -8x+104x+520=136 \\ 96x=136-520 \\ 96x=-384 \\ x=-(384)/(96) \\ x=-4 \end{gathered}`

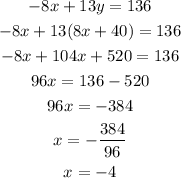
Step 5: Solve for y

`\begin{gathered} y=8x+40 \\ =8(-4)+40 \\ =-32+40 \\ y=8 \end{gathered}`

Step 6: Solve for z.

`\begin{gathered} z=27+3x-2y \\ =27+3(-4)-2(8) \\ =27-12-16 \\ z=-1 \end{gathered}`

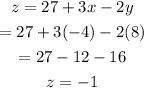
The solution to the system of equations is:

• x=-4

,

• y=8; and

,

• z=-1.