The critical values of a curve f(x) are thepoints in its domain where the derivative f'(x) is zero or not defined.
Given:
It is given that
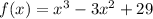
To find critical points first let us find f'(x)
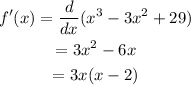
Now on setting f'(x)=0 we have,
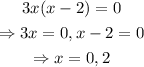
So, the critial values are x=0,2.