Question

The table shows the height of a plant as it grows. A model the data with an equation b. Based on your model, predict the height of the plant at 12 months . A. Y-3 = 5/2 (x-15) ; 57 cm B. The relationship cannot be modeled C. Y-15 = 5/2 (x-30) ; 30 cm D. Y-15 = 5(x-30) ; 60 cm

Answer 1

`\begin{gathered} \text{ A. }y-15=5(x-3) \\ \text{ B. }y=\text{ 60 cm} \end{gathered}`

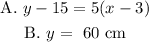
Explanation:

This situation can be modeled by a linear equation since it has a constant rate of change. Linear functions are represented in the slope-point form by:

`\begin{gathered} y-y_0=m(x-x_0) \\ \text{where,} \\ m=\text{slope} \\ (x_0,y_0)\rightarrow_{}\text{ given point} \end{gathered}`

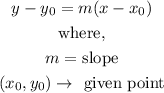
The slope can be calculated as:

`m=(y_1-y_0)/(x_1-x_0)`

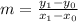
Given the information on the table, we can use the points (3, 15) and (5,25):

`\begin{gathered} m=(25-15)/(5-3) \\ m=(10)/(2) \\ m=5 \end{gathered}`

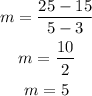
A. Then, by the slope-point form we can model the situation:

`\begin{gathered} y-15=5(x-3) \\ \end{gathered}`

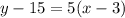
B. Now, to predict the height of the plant after 12 months, substitute x=12 into the equation:

`\begin{gathered} y=5x-15+15 \\ y=5x \\ y=5(12) \\ y=\text{ 60 cm} \end{gathered}`