Answer:

Step-by-step explanation:
If we plot the points in a graph, we can see that they form a line:
Then, we can use the point-slope form of a line.
The slope-point form of a line, given a point P, is:
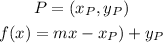
Where
m is the slope
(x_P, y_P) are the coordinates of a point.
To find the slope, we need two points P and Q:
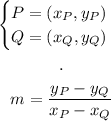
Let's take the points:
P = (1, 18.7)
Q = (2, 19.5)
Then, using the formula for the slope:
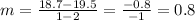
Now, using the slope-point form of a line, with m = 0.8 and P = (1, 18.7):
