Question

G( x )= a(x^2)+bx+cConvert it to vertex form (also known as standard form) by putting the values for a,h and k into the correct boxes.G(x)=a(x-h)^2+kIdentify the vertex(x,y)General form: G( x )=-7 x^2+-9 x +-4 Vertex form: G( x )= Answer for part 1 and coordinate 1 (x- Answer for part 1 and coordinate 2 )^2 +Answer for part 1 and coordinate 3Vertex: (Answer for part 2 and coordinate 1,Answer for part 2 and coordinate 2)

Answer 1

The vertex form of G(x) is

`G(x)=-7(x-(9)/(2))^2-(583)/(4)`

`\text{Vertex}=((9)/(2),-(583)/(4))`

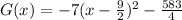
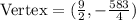
STEP - BY - STEP EXPLANATION

What to find?

Vertex form of the given equation.

Given:

G(x) = - 7x² + -9x + -4

We can re-write the above as:

G(x) = -7x² - 9x - 4

To write the above in a vertes form, we wil follow the steps below:

Step 1

Insert a parenthesis before x² and after 9x.

G(x) = -7(x²-9x) - 4

Step 2

Add/subtract the square half of the co-efficient of x.

That is; half square of -9 = (-9/2)² = 81/4

So that we have:

G(x) = -7(x² - 9x + 81/4) -7(81/4) - 4

Step 3

Simplify

`\begin{gathered} G(x)=-7(x^2-9x+(81)/(4))-7((81)/(4))-4 \\ \\ =-7(x^2-9x+(81)/(4))-(567)/(4)-4 \\ \\ =-7(x^2-9x+(81)/(4))-(567-16)/(4) \\ \\ =-7(x^2-9x+(81)/(4))-(583)/(4) \end{gathered}`

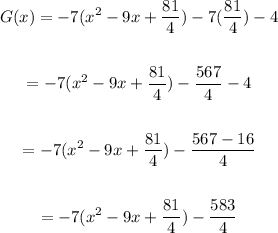
Step 4

Factorize the expression in the parenthesis.

`G(x)=-7(x-(9)/(2))^2-(583)/(4)`

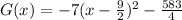
Hence, the vertex form is G(x) = -7(x- 9/2)² + -583/4

The vertex

Given the general formula y=a(x-h)² + + k

The vertex is (h, k).

Comparring the general form to our answer in step 4. Observe that h=9/2 and k=-583/4

Therefore, the vertex is ( 9/2 , -583/4)