Answer:
The acute angle lies between the vectors a=3i+4j and b=7i+j is 45°
Step-by-step explanation:
The given vectors are:
a = 3i + 4j
b = 7i + j
The acute angle between vectors a and and b is given by the formula:
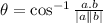
The scalar product of vectors a and b is:
a.b = (3i + 4j).(7i + j)
a.b = (3x7) + (4x1)
a.b = 21 + 4
a.b = 25
The magnitude of a is:
![\begin{gathered} |a|=\sqrt[]{3^2+4^2} \\ |a|=\sqrt[]{9+16} \\ |a|=\sqrt[]{25} \\ |a|=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jksiocoantjggwrrcxo8ky6q2nklja9rft.png)
The magnitude of b is:
![\begin{gathered} |b|=\sqrt[]{7^2+1^2} \\ |b|=\sqrt[]{49+1} \\ |b|=\sqrt[]{50} \\ |b|=5\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/db3mknakpylutv6e83hgufnhsh64a9vwva.png)
Substituting the values of a.b, |a|, and |b| into the formula for the acute angle.
![\begin{gathered} \theta=\cos ^(-1)(a.b)/(|a\Vert b|) \\ \theta=\cos ^(-1)\frac{25}{5*5\sqrt[]{2}} \\ \theta=\cos ^(-1)\frac{25}{25\sqrt[]{2}} \\ \theta=\cos ^(-1)\frac{1}{\sqrt[]{2}} \\ \theta=45^0 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/14a9fx0g86ny9k3u3w0kav1xisto7k610r.png)
Therefore, the acute angle lies between the vectors a=3i+4j and b=7i+j is 45°