Question

Determineroots3) Describe end BehaviorDraw QUICh Sketch.of polymonialfl X=-7X" +22

Answer 1

We are given the polynomial

`\text{ -7x}^4+2x^3`

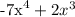
Find the roots:

To find the roots of this polynomial, we want to solve the following equation

`\text{ -7x}^4+2x^3=0`

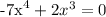
On the left side, we can factor the polynomial as follows

`x^3\cdot(\text{ -7x+2) =0}`

This leads to the following two equations

`x^3=0`

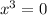
with solution x=0, and the equation

`(\text{ -7x+2)=0}`

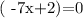
by subtracting -2 from both sides , we get

`\text{ -7x= -2}`

Finally, by dividing both sides by -7, we get

`x=(2)/(7)`

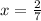
So, the roots of this polynomial are x=0 and x=2/7.

Describe the end behavior:

To describe the end behavior of a polynomial we should first see how the polynomial is written

`\text{ -7x}^4+2x^3`

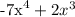
In here, we see that we have a power of 4 and a power of 3. Consider that the power of 4, as x grows bigger and bigger (or smaller and smaller) the power of 4 will dominate the behavior of the polynomial as x⁴ grow bigger and bigger than x³. So, we can forget the other part and focus on the polynomial

`\text{ -7x}^4`

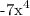
Note that as x is a positive number, then x^4 is also a positive number. So as x grows bigger and bigger, we would get a more negative number, since we are multiplying -7 (a negative number) with a really big positive number (x^4). Then this polynomial will go to - infinity as x grows bigger and bigger.

Also, to understand the end behaviour, we should see how the polynomial behaves as x becomes a really negative number. As before, we can only focus on the polynomial

`\text{ -7x}^4`

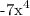
note that if x is a negative number, x^4 is again a positive number. So, as x becomes more negative (approaching - infinity) the number -7x^4 would once again be a negative number. So, the end behavior as x goes - infinity is also - infinity.

Sketch:

For the sketching, we will use a sketchin software, so the polynomial would look like this