Question

Suppose a point has polar coordinates (6,5pi/6)with the angle measured in radians.Find two additional polar representations of the point.Write each coordinate in simplest form with the angle in (-2pi, 2pi).

Answer 1

To find the additional polar representation of a giving point we use the following

1. By adding or subtracting a multiple of 2π to θ

2. By using a negative radius r, and adding an odd multiple to π

Giving the polar coordinates

`(6,(5\pi)/(6))`

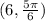
The additional coordination will be by adding 2π to θ

`\begin{gathered} (6,(5\pi)/(6)+2\pi) \\ \\ (6,(17\pi)/(6)) \end{gathered}`

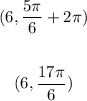
Hence one addition coordinate is (6,17π/6)

To find additional polar coordinates,

We subtract 2π from θ

`\begin{gathered} (6,(5\pi)/(6)) \\ \text{Then} \\ (6,(5\pi)/(6)-2\pi) \\ \\ (6,(5\pi-12\pi)/(6))=(6,-(7\pi)/(6)) \end{gathered}`

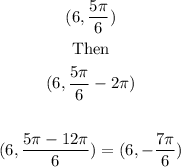
Hence, another additional coordinate is (6,-7π/6 )

Therefore, the two additional polar coordinates are (6,17π/6) and (6,-7π/6 )