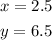Question

Use the graph to estimate the solution 8. y = x + 4 y = 3x - 1

Answer 1

The Slope-Intercept form of the equation of a line is:

`y=mx+b`

Where "m" is the slope of the line and "b" is the y-intercept.

1. In this case, you have the first equation of the line in Slope-Intercept form:

`y=x+4`

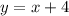
You can identify that:

`\begin{gathered} m=1 \\ b=4 \end{gathered}`

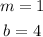
The line intersects the x-axis when the value of "y" is:

`y=0`

Substituting this value into the equation and solving for "x", you get that the x-intercept is:

`\begin{gathered} 0=x+4 \\ x=-4 \end{gathered}`

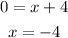
Now you graph the first line.

2. The second line is:

`y=3x-1`

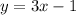
You can see that:

`\begin{gathered} m=3 \\ b=-1 \end{gathered}`

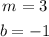
Find the x-intercept applying the same procedure used for the first line:

`\begin{gathered} 0=3x-1 \\ 1=3x \\ \\ x=(1)/(3) \\ \\ x\approx0.33 \end{gathered}`

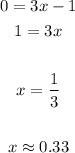
Now you can graph the second line.

See the graph below:

The point of intersection between the lines is the solution of the System of equations. Then, you can estimate that the solution is:

`\begin{gathered} x=2.5 \\ y=6.5 \end{gathered}`