Question

Hello,I am a grade 10 student and I am looking for some help on physics equations (acceleration, time distance, etc). I am also looking in to calculating speed, distance and time. I am studying for an exam and I have a preparation worksheet.

Answer 1

1.3 times faster

Explanation:

Given:

Distance ostrich = 56 m

Time ostrich = 14.5 s

Initial velocity = 0 m/s

To calculate the final velocity of the ostrich we use the following formula:

`\begin{gathered} d=0.5(v_f+v_i)\Delta t \\ \\ \text{ we solve for }v_f \\ \\ 56=0.5(0+v_f)14.5 \\ \\ 56=7.25v_f \\ \\ v_f=(56)/(7.25)=7.7\text{ m/s} \end{gathered}`

Now, we calculate the average velocity of the ostrich, like this:

`\begin{gathered} v_o=(v_i+v_f)/(2)=(0+7.7)/(2) \\ \\ v_o=3.9\text{ m/s} \end{gathered}`

We calculate the time it would take the ostrich to travel 100 meters with the following formula:

`\begin{gathered} d=0.5(v_(f)+v_(i))\Delta t \\ \\ \text{ we replacing} \\ \\ 100=0.5\left(0+7.7\right)\Delta t \\ \\ \Delta t=25.9\text{ sec} \end{gathered}`

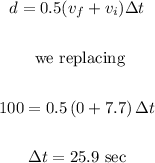
now we calculate the time of the cheetah knowing that it takes 5.7 seconds less:

`\begin{gathered} t_c=t_o-5.7 \\ \\ t_c=25.9-5.7=20.2\text{ sec} \end{gathered}`

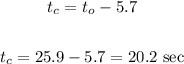
Now, we can calculate the final velocty of the cheetah using the following formula:

`\begin{gathered} d=0.5(v_(f)+v_(i))\Delta t \\ \\ \text{ we replacing} \\ \\ 100=0.5\left(v_f+0\right)20.2 \\ \\ v_f=(100)/(10.1) \\ \\ v_f=9.9\text{ m/s} \end{gathered}`

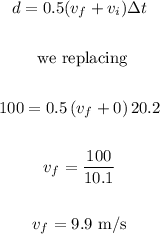
Now we calculate the average velocity, like this:

`\begin{gathered} v_c=(v_i+v_f)/(2)=(0+9.9)/(2) \\ \\ v_c=4.95\text{ m/s} \end{gathered}`

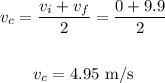
we calculate the ratio between the two to know how many times the cheetah is faster:

`r=(4.95)/(3.9)=1.3`

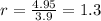
Therefore, the cheetah is 1.3 times faster than the ostrich.